Landscape Ecology - Lecture Notes

Quantifying Landscape
Pattern: Methods and Applications
Landscape Pattern Analysis - Spatial Statistical
Methods
 Regionalized variable theory
Regionalized variable theory
- Regionalized variable theory (Matheron 1963) provides an
important theoretical basis for spatial statistics and
geostatistics, which recognizes that observations taken at
short distance from each other are more alike, i.e., have
lower variances, than those taken further apart.
- Regionalized variable theory has implications for field
sampling and experimentation. Indeed, geostatistical
principles are generating a rethinking of conventional field
experimentation.
 Spatial Statistics
Spatial Statistics
- The objectives of spatial statistics are: to describe how
things are distributed in space (e.g., random, clustered,
uniform), and to determine if spatial proximity (spatial
autocorrelation) is playing a causal role in the observed
distribution.
- It is important to distinguish pattern caused by
environmental or spatial heterogeneity from that caused by
spatial dependence or autocorrelation.
 Geostatistics
Geostatistics
- Geostatistics is a set of statistical tools that detect,
model and estimate spatial dependence or pattern of
variables.
- Geostatistics allows for optimized estimation of such
"regionalized variables" at unsampled locations through
quantification of its spatial dependence structure.
How does geostatistics differ from traditional
statistics?
- Commonly used statistical tests (t-test, ANOVA, etc.)
assume independence and normal distribution
of sample values. Geostatistical tests specifically look
for and quantify spatial dependence.
- The difference between geostatistical and conventionally
used assumptions is that the former recognizes the
existence of a spatial relationship for (co)variances
which depends only on the separation vector h. Thus,
if observations separated by different distances are
compared, their expected (co)variances may be unequal.
Why is this beneficial to ecological studies?
- Space and time dependence and continuity are inherent in
ecological phenomena. Organisms are not distributed
randomly across their environment. Environmental variables
like temperature and soil moisture do not change from one
location to the next in an unrelated way.
- Spatial dependence or temporal dependence in one
direction or another may indicate an underlying ecological
process and direct further research.
- The application of geostatistical tools may cause
erroneous results if: (i) if the sampling domain does not
adhere to the intrinsic hypothesis, or (ii) geostatistical
tools are inappropriately used.
 Autocorrelation indices:
Autocorrelation indices:
where xi and xj are the values of grid cells i
and j, and all other parameters are defined as in the
equation for Moran's I.
- It seems desirable to use the two commonly used indices
together in that Moran's I is intended to measure the degree
of correlation between neighboring sites, whereas Geary's c
measures how different they are. The degree of autocorrelation
may be indicative of spatial distribution of landcover types
(aggregated, regular, or random) or patchiness in landscape
pattern (e.g., Legendre and Fortin 1989, Qi
and Wu 1996).
Spatial pattern
Moran's
I Geary's c
Positively
correlated
0 < I <
1 0 < c
< 1
(similar, smooth,
regionalized)
Negatively
correlated
-1 < I < 0
1 < c < 2
(dissimilar, contrasting,
checkerboard)
Spatial autocorrelation indices, Moran's I and Geary's c
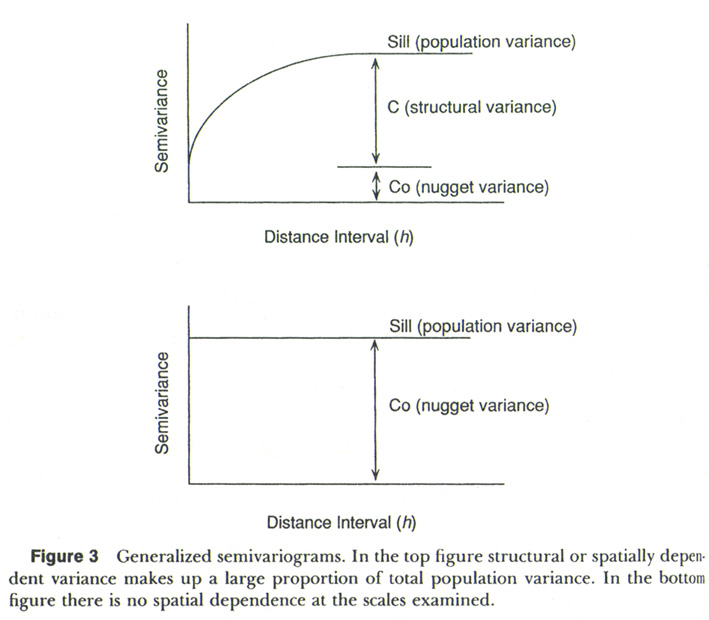
 Semivariance
analysis:
Semivariance
analysis:
- Semivariance analysis provides another means for examining
autocorrelation in spatial data, which does not require
second-order stationarity (while autocorrelation measures such
as Moran's I do).
- Semivariogram can define the range or distance over
which spatial dependence exists.
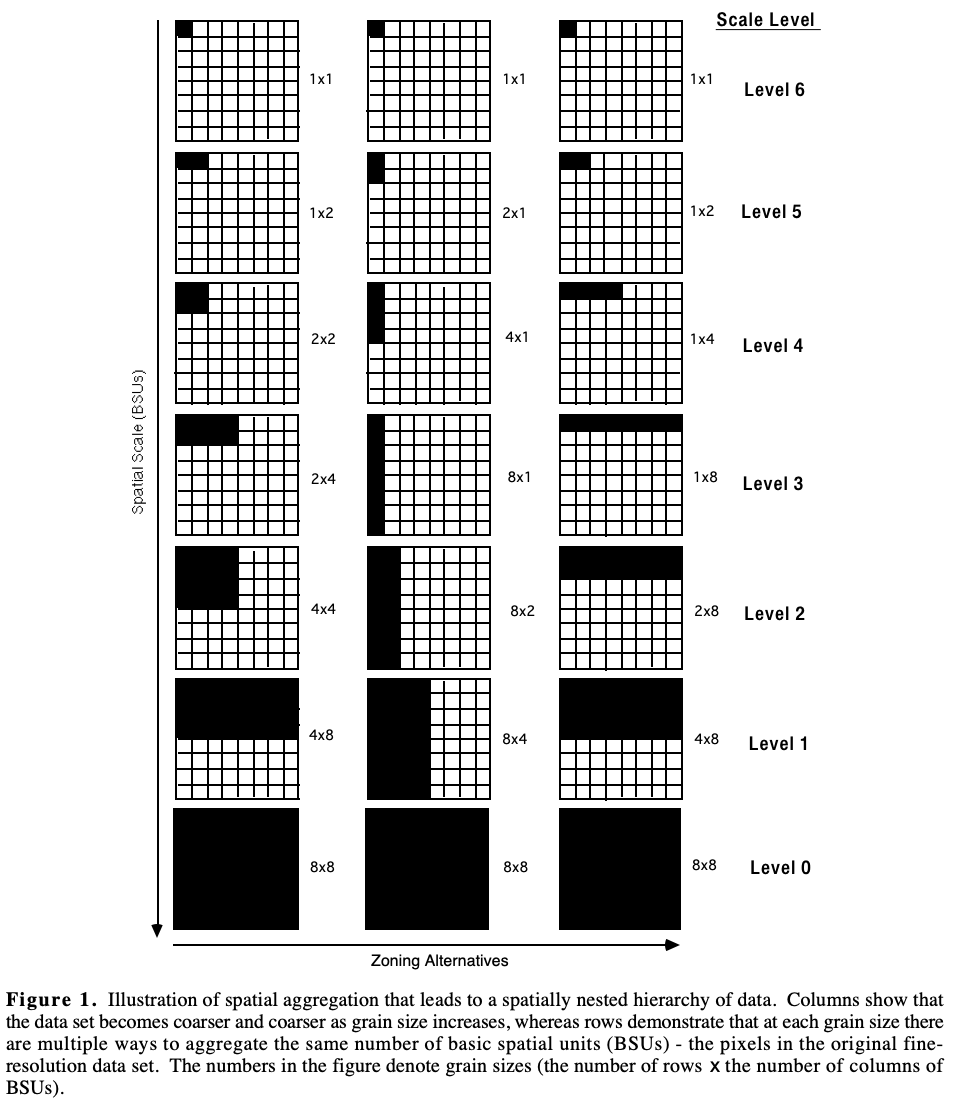
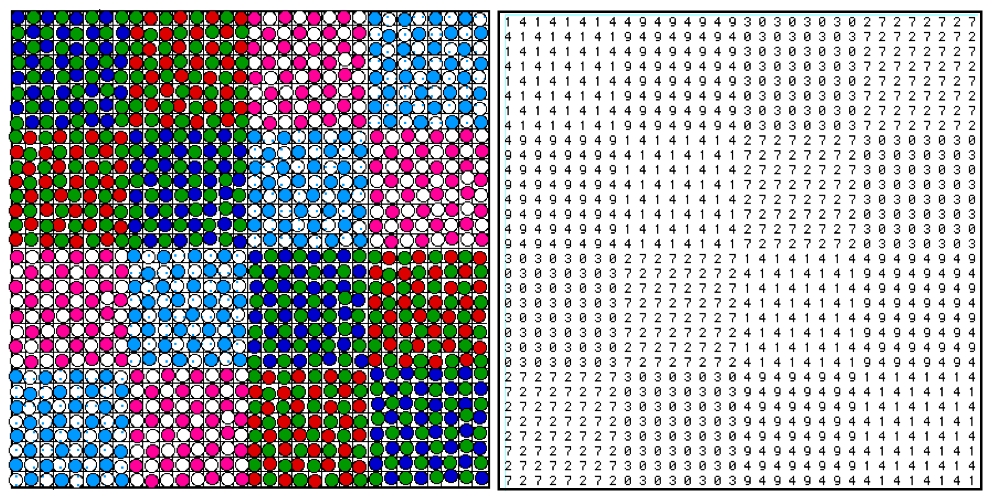
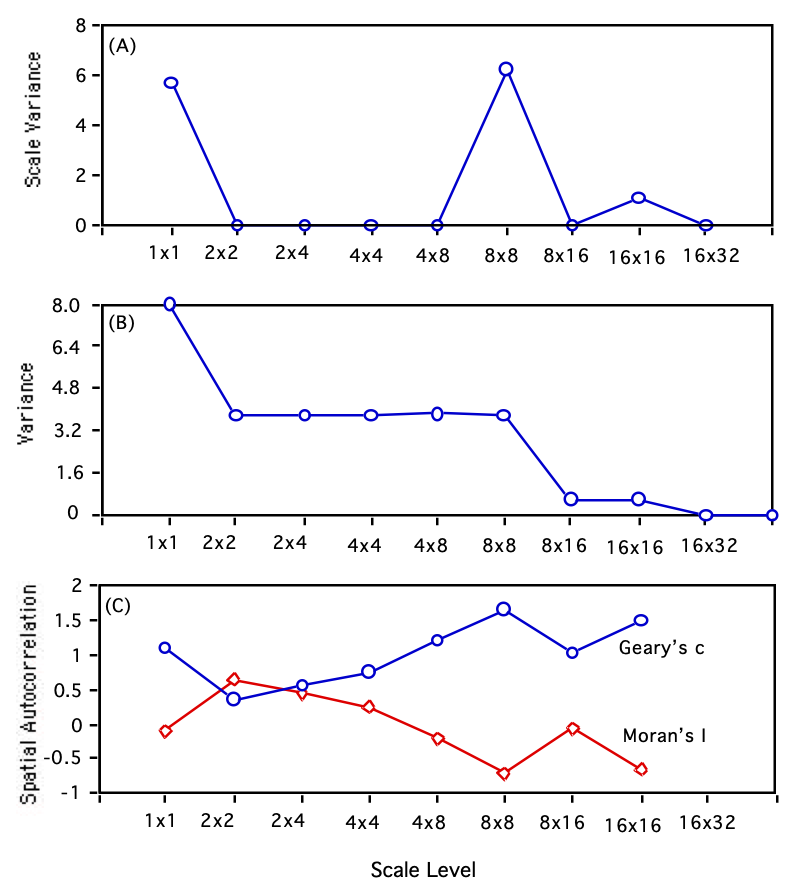
 Scale
variance analysis
(Moellering and Tobler 1972):
Scale
variance analysis
(Moellering and Tobler 1972):

References:
- Wu, J. G., D. E. Jelinski, M. Luck, and P. T. Tueller. 2000. Multiscale
analysis
of
landscape
heterogeneity:
Scale variance and pattern metrics. Geographic Information
Sciences 6:6-19.
- Fortin, M.-J., M. R. T. Dale, and J. ver Hoef. 2002. Spatial
analysis in ecology. Encyclopedia of Environmetrics 4:2051-2058.
- Fortin, M.-J. and M. R. T. Dale. 2005. Spatial Analysis:
A Guide for Ecologists. Cambridge University Press, Cambridge.
- Griffith, D. A. 2012. Spatial statistics: A quantitative
geographer's perspective. Spatial Statistics 1:3-15.
Dr. Wu's Landscape Ecology Homepage