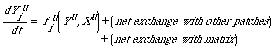Landscape Ecology - Lecture Notes

Landscape
Pattern and Population Processes
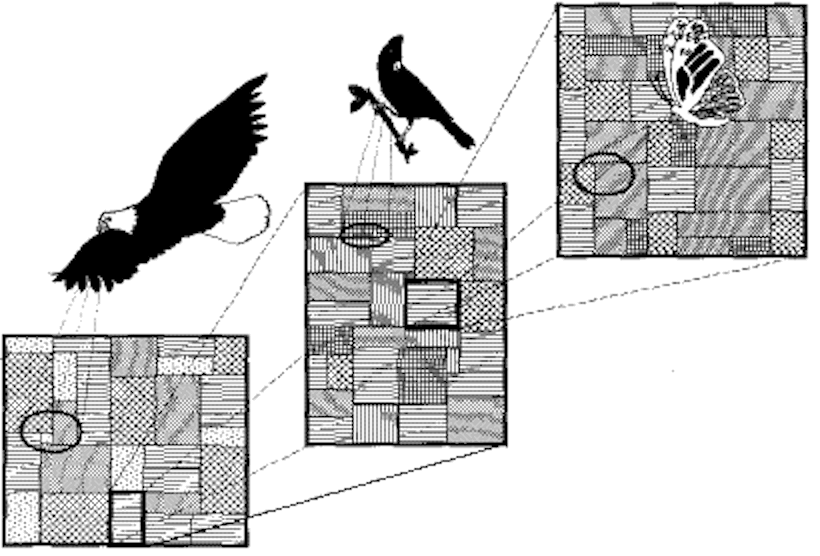
I. Scale-Dependent
Relationships between Organisms and Landscape Pattern
(From FRAGSTATS mannual 1995)
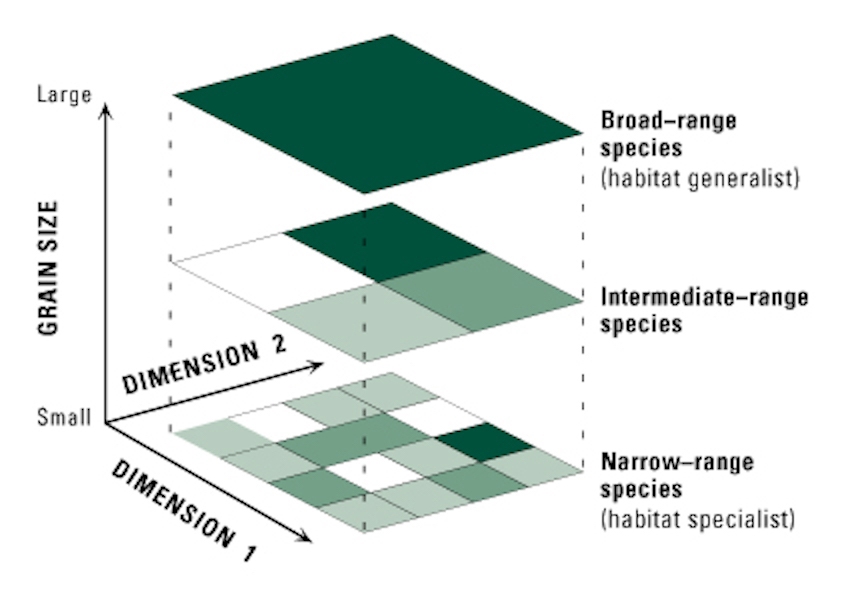
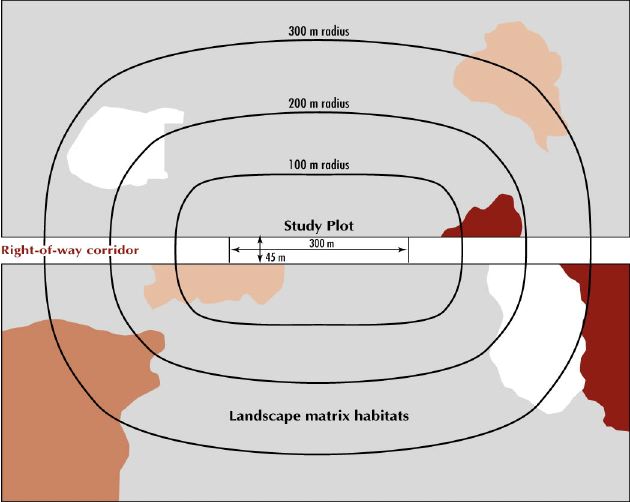
(Turner et al. 2001)
(Turner et al. 2001)
II. Metapopulation Dynamics
1. What is a
metapopulation?
- Original definition by Richard Levins (1970): "a
population of populations which go extinct locally and recolonize".

 [http://www.hsph.harvard.edu/faculty/richard-levins/]
[http://www.hsph.harvard.edu/faculty/richard-levins/]
- History:
- - Wright (1940): Population genetics in spatially
heterogeneous environment - A basis for metapopulation
genetics
- - Andrewartha and Birch (1954): Local extinction and
recolonization in spatially heterogeneous populations;
density-independent population dynamics
- - MacArthur and Wilson (1963, 1967): Extinction , colonization
, area effect, distance effect, rescue effect, target effect
- - Levins (1970), Levins and Culver (1971), Levin (1976): Mathematical
formulation
- Two Views of Metapopulations (Hanski and Gilpin
1997)
- Narrow classical view of
metapopulations:
- Levins's original concept of a metapopulations as a
population of populations, analogous to a population of
individuals with finite lifetimes.
- Broader view of
metapopulations:
- Any assemblage of discrete local populations with
migration/dispersal among them, regardless of local
population turnover (Hanski and Gilpin 1997).
- Or: A system of subpopulations that are spatially
separated by unsuitable environment (resulting in
local extinctions) and functionally connected by
dispersal (leading to recolonization).
- Metapopulation
Terminology (Hanski, I., and D. Simberloff. 1997. The
metapopulation approach, its history, conceptual domain, and
application to conservation. Pages 5-26 in I. Hanski and M.
E. Gilpin, editors. Metapopulation Biology: Ecology,
Genetics and Evolution. Academic Press, San Diego)


2. Metapopulation
Types
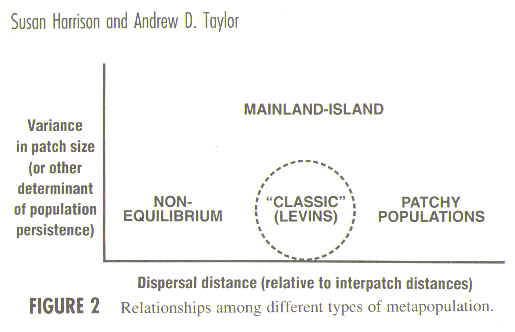
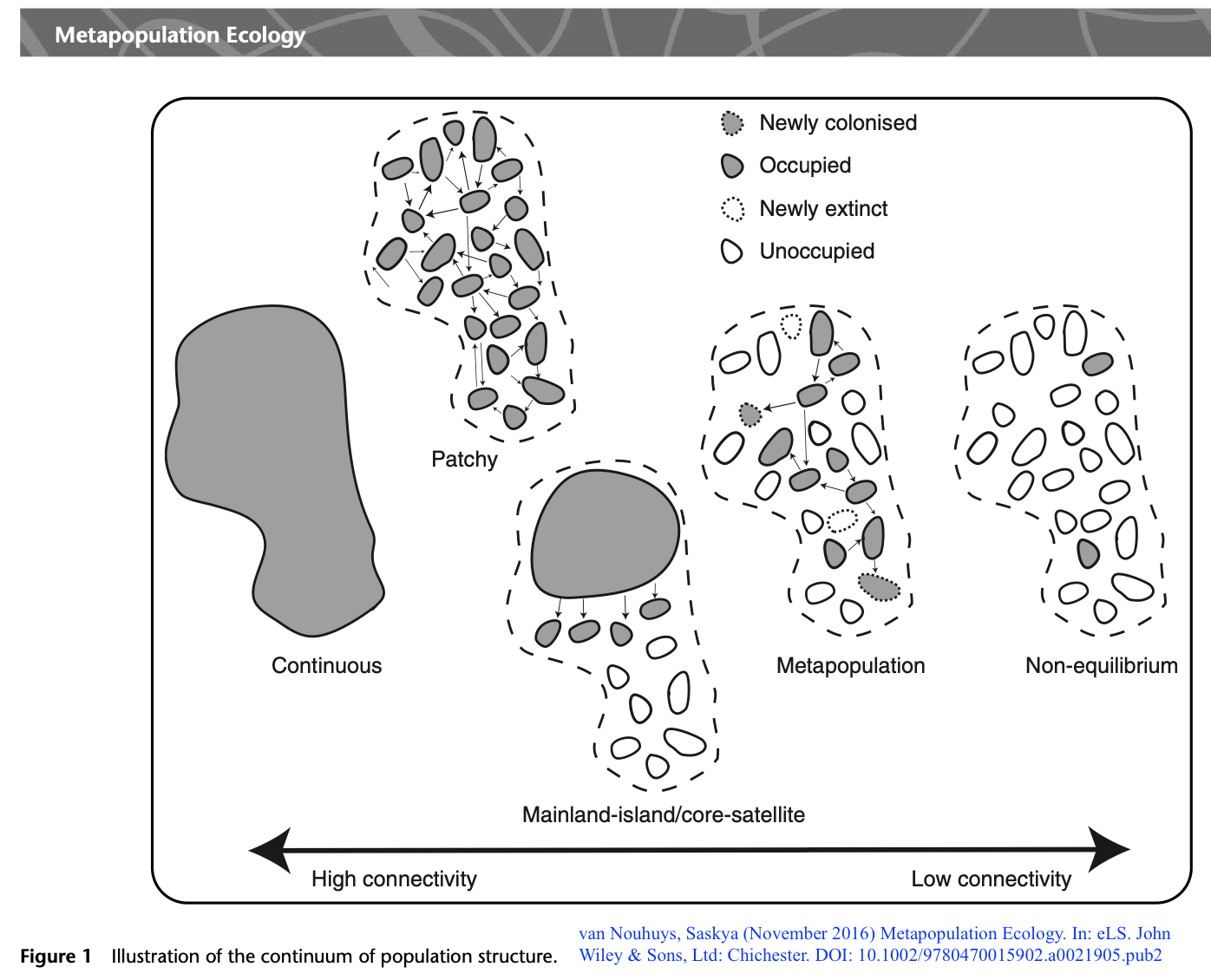
Metapopulation types (Harrison and Taylor 1997)
- Classic (Levins) metapopulations
- Mainland-island metapopulations
- Patchy populations
- Nonequilibrium metapopulations
- Intermediate case
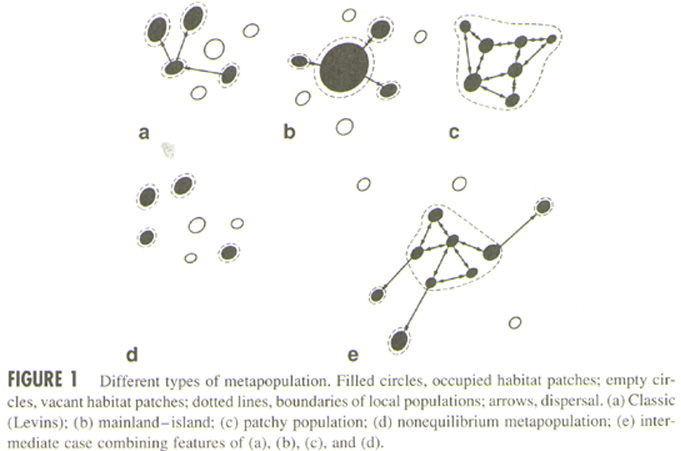
Relationship among different types of metapopulations (Harrison
and Taylor 1997)
3. Modeling Approaches to Metapopulation
Dynamics
- - Patch-Occupancy Models (Non-Spatial)
- - Diffusion-Reaction Models (Quasi-Spatial)
- - Patch Demographic Models (Quasi-Spatial)
- - Gap Models (Quasi-Spatial)
- - Spatial Patch Dynamics Models (Spatially Explicit)
(1). Non-Spatial Patch-Implicit Models (or Non-Spatial
Patch Models)
They include mainly the so-called patch-occupancy models in
which the state variables are usually the proportions of patches
occupied and unoccupied by a species' populations or by
different species (Levins, 1970; Gilpin and Hanski, 1991). These
models deal with a large number of patches and involve both
single-species dynamics and multi-species interactions.
Mathematically, patch-occupancy models mostly take the
analytical approach. The simplest model of this type is of the
form
dp/dt = m p (1 - p) - e p
where p is the proportion of patches occupied by the
species and m and e are constants that are related to
the colonizing ability and extinction rate of the species,
respectively. When the metapopulation reaches an
equilibrium state, i.e., dp/dt = 0, the equilibrium value of p
is:
(2). Quasi-Spatial, Patch-Explicit Models (or Quasi-Spatial
Patch Models)
They may be further broken into three subcategories:
diffusion-reaction models, patch demographic models, and gap
models. Diffusion-reaction models usually have population
densities as state variables and take into account such spatial
aspects as patch size and interpatch distance indirectly (e.g.,
Levin, 1976; Okubo, 1980). A general formulation of these models
is as follows (as per Levin, 1976):
in which Yu is the vector (Y1u,
Y2u, ..., Ynu) of
state variables for a given patch u, Xu the vector
(X1u, X2u, ..., Xnu) of
parameters accounting for the same patch, and fu the
specific functional relationship.
Population density or other variables of interest may be
coupled with the patch demographic model in the following
general form (Levin 1976):

Gap models include a large host of computer simulation models
of forest dynamics (e.g., Botkin et al., 1972; Shugart and
West, 1977). These models usually spatially explicit only on
the vertical dimension; the simulation plot -- gap is
explicitly considered, but not the entire model area. A
detailed and comprehensive review on these models can be found
in Shugart (1984).
(3). Spatially Explicit Patch Models (Spatial Patch Models)
- Lefkovitch, L. P. and L. Fahrig (1985). “Spatial
Characteristics of Habitat Patches and Population Survival.”
Ecological Modelling 30: 297-308.


4. Metapopulation Theory: Some Important Aspects
- - Hierarchical structure and multi-scale dynamics
- - Spatial scales: Local, landscape, and biogeographical scales
- - Time scales: a critical problem in defining and
understanding metapopulation dynamics
- - Two major driving forces: local extinction and interpatch
colonization
- - Patch dynamics and system stability
- - Metapopulation processes and MVP
- - Integration of landscape pattern and ecological processes
- Importance in Biodiversity Conservation: Island
Biogeography Theory to Metapopulation Theory
5. Problems with the Metapopulation
Approach
- Comparing metapopulation theory and landscape mosaic
approaches
The
concept
of metapopulation, a
population of subpopulations that go extinct locally and
recolonize regionally, resembles the theory of island biogeography
in that both consider extinction and colonization as the two key
processes. However, the former is concerned with population dynamics and species
persistence while the latter focuses primarily on species diversity and turnover.
Also, sources for species colonization in most metapopulations
are neighboring habitat patches that themselves are subject to
local extinctions.
The classic (or Levins) metapopulation
models are commonly known as “patch-occupancy” models in which
the proportion of habitat patches occupied by a species is
modeled as a function of local extinction and inter-patch
colonization (Fahrig 2007). These models assume that there
are an infinite number of identical habitat patches in the
landscape, and that within-patch population dynamics and the
landscape matrix are not important to metapopulation
dynamics. The classic metapopulation models are not really
spatial models. More spatially sophisticated
metapopulation modeling approaches have been developed in the
past several decades. For example, many population models
based on diffusion-reaction
equations, which consider both local population
processes and patch attributes (e.g., size, relative distance to
other patches), are relevant to the study of metapopulation
dynamics. However, these are quasi-spatial models which can not
explicitly consider the locations and geospatial relations of
habitat patches and the heterogeneity of the landscape
matrix. The prevailing metapopulation modeling approach
now is the so-called spatially realistic
metapopulation models that incorporate the
effects of habitat patch size and isolation on extinction and
colonization rates into the classic metapopulation models.
While these models are spatially realistic, like the classic
models they are concerned only with two states of habitat
patches: presence and absence of a species under study, not with
population processes within habitat patches. Also, the heterogeneity of the landscape
matrix is usually ignored in spatially realistic
metapopulation models.
Metapopulation theory has been
increasingly used in conservation biology in the past three
decades, replacing the prominent role of island biogeography
theory. However, its use for the practice of biodiversity
conservation is limited by its species-specific
focus and inadequate consideration of the heterogeneity of landscape matrix and
socioeconomic processes.
In reality, populations neither live in habitat patches that can
always be neatly delineated nor reside in a homogeneous
landscape matrix. Rather, they are situated in
heterogeneous and dynamically complex landscapes that are shaped
by a myriad of physical, biological, and socioeconomic
processes. Thus, the metapopulation approach is useful,
but certainly not adequate for achieving the overall goal of
conserving all levels of biodiversity.
III. Summary of Effects of Landscape
Fragmentation on Population Dynamics and Species Persistence
[Excerpt from: J.
Wu
(2009). Ecological dynamics in fragmented landscapes. In:
Simon A. Levin (ed). Princeton Guide to Ecology. Princeton
University Press, Princeton.]
In reality
landscape fragmentation simultaneously leads to habitat loss and habitat isolation. These
changes can certainly affect the demographic and genetic
processes of populations. A great number of
theoretical and empirical studies have been carried out to
understand how habitat fragmentation affects population
dynamics and species persistence in the past several
decades. This section provides an overview of the
major findings up to date.
Findings
of the effects of landscape fragmentation on population
dynamics and species persistence have been, more often than
not, incongruent because of several reasons. First,
the term “landscape (or
habitat) fragmentation” is often used to denote
both habitat loss
and habitat isolation
(i.e., habitat fragmentation per se), and consequently the
effects of the two factors are confounded in the results of
such studies. Second, various measures that reflect different
aspects of landscape pattern at different scales have been
used to quantify habitat fragmentation. Some measures
focus on habitat loss, others are indicative of changes in
habitat configuration, and still others are mixtures of
both. Also, habitat fragmentation is measured either
at the scale of individuals patches (as in most
metapopulation models) or the scale of the entire landscape
(as in most landscape ecological studies). Third, different theories and models
have different assumptions about what is important in
fragmented landscapes in terms of population dynamics and
species persistence, and these differences in assumptions
often translate into discrepancies in results.
Nevertheless, studies in recent decades have produced
several important findings.
The relative effects of habitat
loss and habitat isolation have been one of the
central topics. Increasing empirical evidence
indicates that habitat
loss usually has much stronger effects on
population dynamics and species persistence than habitat
isolation. In general, the effects of habitat isolation tend to be stronger
when the total amount of habitat in the landscape is small
and when the species under consideration have limited
dispersal abilities. The effects of habitat loss are
consistently negative whereas those of habitat isolation
can be either negative or positive depending on the
idiosyncrasies of the landscape pattern (e.g., the spatial
configuration of habitat patches) and the species under
consideration (e.g., abilities for local competition and
regional dispersal). The negative effects of habitat
loss are easier to understand because the removal of habitat
usually results in reduction in the number of species, the
abundance of populations, and the carrying capacity of the
landscape.
The
effects of fragmentation per se, however, are more complex
because the outcome depends on how the species responds to
the specific features of the fragmented habitat and altered
interactions with other species in the landscape. The
negative effects of habitat isolation may be caused by the
disruption of dispersals, increased local extinction rates
in small patches, and detrimental
edge effects. The positive effects of habitat
isolation may be attributable to relaxed interspecific competition, reduced predation, and disrupted spreading of
disturbances. However, it is important to
note that the effects of
spatial patchiness occurring naturally are different from
the effects of habitat fragmentation by human activities.
In
the latter situation, species usually do not have enough
time to adapt to the newly changed environment, and thus
positive fragmentation effects are less likely, especially,
for non-edge species.
The size of habitat patches has
significant effects on population dynamics and species
persistence simply because large patches tend to
have larger populations (thus with lower extinction
probabilities) and more species (due to both pure area
effect and higher habitat diversity). In general, patch size has strong
positive effects on interior species that require
sufficiently large and relatively stable habitat. As
patch size increases, the relative area of edge habitat
decreases, resulting in negative effects of patch size on
edge species. For generalist
species that do not distinguish between edge and interior
habitat, the effects of patch size usually are
insignificant. The effects of patch size on population
dynamics and species persistence may also vary with species
that have different behavioral characteristics. For
example, some studies have suggested that more mobile or
dispersive species would be less strongly affected by
landscape fragmentation. However, recent studies show
that the opposite may be true when more mobile species
suffer severe dispersal
mortality in the landscape matrix (Fahrig 2003,
2007). Other patch characteristics such as shape,
orientation, and boundary conditions can also affect
population processes. Their effects seem less
significant than those of patch size, and usually are even
harder to generalize across different species and habitat
types.
Landscape connectivity,
which is conversely related to habitat isolation, plays a crucial role in
maintaining population abundance and species persistence
by affecting the movement of organisms and propagules,
dispersal mortality, and gene flows. Studies from
landscape ecology based on percolation theory have suggested
that, as habitat area decreases to some critical value,
landscape connectivity drops abruptly, indicating a possible
extinction threshold
for species with limited dispersal ability or high dispersal
mortality (With 2004). This finding corroborates the
hypothesis that the effects of habitat isolation on
population and species dynamics tend to be more important
with decreasing habitat amount in the landscape. Thus,
landscape connectivity exhibits threshold behavior and is
species- or process-specific. Corridors, as a means of
increasing habitat connectivity,
can promote species persistence
(by enhancing re-colonization) and genetic integrity (by
preventing genetic drift and bottleneck effects).
However, corridors may also increase the spread of diseases and other
disturbance agents across the landscape.
Back to Dr. J. Wu's Landscape Ecology
Homepage